Rechercher dans le site :

Traduction/Translation/Traduko/Traducción/Übersetzung/Traduzione

Identifiez-vous pour accéder à la partie privée du site ou le modifier.

Déconnexion.

Ĉu vi parolas esperanton ?

 

Dernière mise à jour le 22/10/2023

Une expérience de physique : oscillation du pendule Micro:bit

Montage expérimental

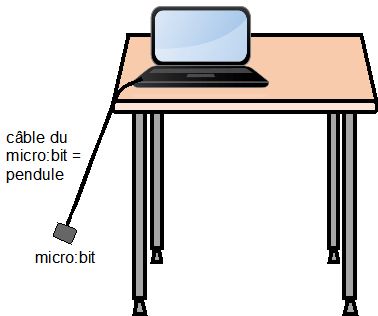
Le capteur d’accélération permet de mesurer l’accélération, dans un axe quelconque (X, Y ou Z). Comme la position du pendule (= micro:bit et son câble) varie en fonction du temps, l’accélération mesurée varie aussi,et on peut mesurer l’oscillation (amplitude et fréquence) de ce pendule.

 

Logiciel utilisé et résultats

Les images ci-dessous sont des copies d’écran de MGW32 (logiciel pour Windows) (http://sciencexp.free.fr/logwin32/logwin32.htm). On a réglé la voie principale avec le pilote bibdyn_microbit_PB_rapide.dll (mesures en accélération X = horizontale), puis on a réglé le temps entre 2 mesures à 100 ms, et 500 mesures à faire. Après le déclenchement des mesures, on a écarté le pendule de la verticale, puis on l’a relâché.

Visuellement, on voit que les oscillations du pendule s’amortissent peu à peu. Il semble que la période ne varie pas ou peu. C’est ce qu’enseigne la théorie : la période du pendule est indépendante de l’amplitude de l’oscillation, et de la masse du pendule, mais ne dépend que de la longueur l du pendule (et de l’accélération de la pesanteur g) : T = 2*pi*racine(l/g)

 

Calcul de la période

On peut calculer la période en divisant l’intervalle de temps entre plusieurs maximums par le nombre de périodes ; pour avoir le maximum de précision, le mieux est de prendre le premier et le dernier maximum de l’enregistrement.

En 20 secondes, il y a eu 12,7 cycles d’accélération horizontale (approximativement). La période est donc 20/12,7 = 1,57 secondes.

(Attention à la composante de l’accélération mesurée : l’accélération verticale a une période deux fois plus petite que l’accélération horizontale !)

Confirmation de l’invariance de la période par le logiciel PAST

PAST est un logiciel d’analyse statistique (https://folk.uio.no/ohammer/past/). On peut coller les valeurs à partir de MGW32 dans PAST :

- Dans le menu de la fenêtre graphique de MGW32, choisir Editer / Copier (virgule décimale)

- Dans PAST, choisir Edit / Paste

Le menu Time Series / Spectral analysis / Simple periodogram permet d’obtenir le « périodogramme » : les abscisses sont les fréquences possibles, et les ordonnées sont la puissance de l’amplitude des sinusoïdes correspondant à ces fréquences.

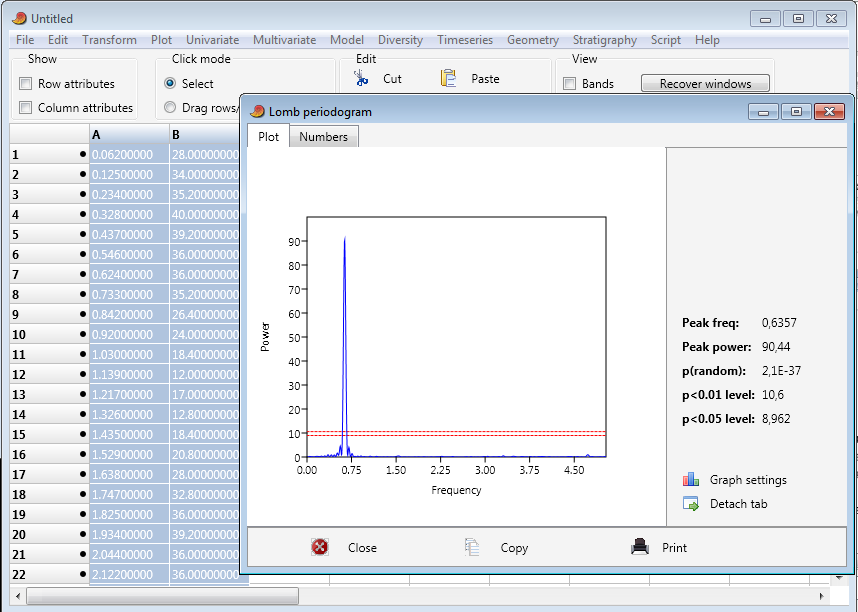
On voit que le pic de fréquence le plus important est à 0,6357 Hz, donc la période est 1/f, soit 1/0,6357 = 1,573 s, ce qui est proche de la valeur trouvée précédemment, 1,57 s. Comme ce pic est très pointu, on peut dire que la fréquence ne varie pas lors de l’amortissement.

 

Pour aller plus loin dans l'expérience du pendule

La carte Micro:bit est très légère, le câble USB aussi, et on ne sait pas très bien où est le centre de gravité du système. Pour essayer de voir que la période est proportionnelle à la racine carrée de la longueur, il faut savoir précisément la longueur du pendule, donc connaître la position du centre de gravité.
On peut fixer une masse assez lourde à l’extrémité du pendule (par exemple un gros boulon fixé à l’extrémité du câble USB, près de la carte Micro:bit). Comme cette masse sera beaucoup plus lourde que l’ensemble (câble + carte), on pourra considérer que la longueur du pendule est la distance entre le bord de la table et la masse ajoutée.

 

Détermination de g

A partir de la relation T = 2*pi*racine(l/g) on peut calculer g = l * 4* π²*f². Ici, avec une longueur de 0,65 m et une période de 1,57 s, on obtient g=10,37 m.s^-2 ; cette valeur est imprécise à cause notamment de l’imprécision sur la longueur du pendule (où est précisément le centre de gravité ? bien que léger par rapport à la masse ajoutée, le câble USB est pesant, de même que la carte Micro:bit).

Relation entre période et longueur du pendule

On peut constater assez facilement que plus le pendule est long, plus grande est la période. Mais est-ce que la période est proportionnelle à la longueur du pendule, ou bien est-ce une relation non proportionnelle ?

On peut faire varier la longueur du pendule (= la longueur du câble USB entre la carte Micro:bit et l’axe de rotation). Un exemple de résultats est donné ci-dessous.

 

L	T
0,67	1,57
0,52	1,43
0,4	1,24
0,28	1,03

 

La modélisation par un tableur permet de constater que lorsqu’on demande la modélisation par la fonction puissance (Y = a*x^b), la meilleure approximation donne une puissance d’environ 0,5 (le coefficient b précédent vaut 0,5), ce qui signifie que la période est proportionnelle à la racine carrée de la longueur du pendule.

 

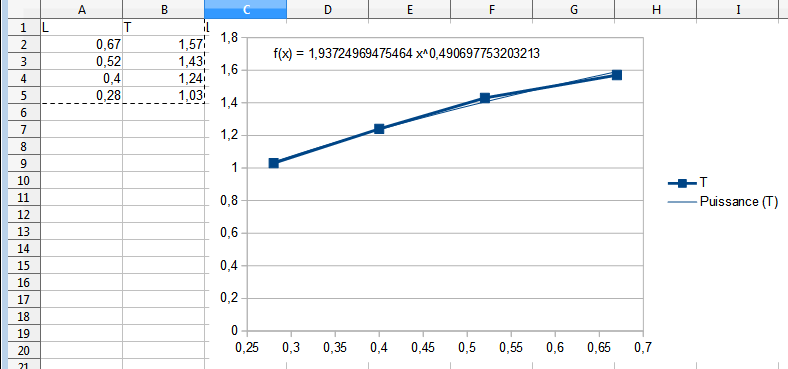
Le coefficient a précédent vaut ici 1,937.

Dans la relation T = 2*pi*racine(l/g), c’est la valeur de 2*pi/racine(g) , qui vaut effectivement environ 2.